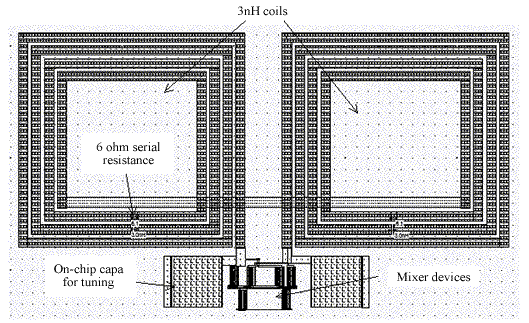
Pour diverses applications radio-fréquence on a besoin de transformer des fréquences en fréquences plus hautes au plus basses, tout en gardant la même amplitude. Générer directement des hautes fréquences (900MHz, 1.8GHz pour la téléphonie mobile par exemple) consommerait beaucoup trop d'énergie. On préfère utiliser un circuit qui transforme une basse fréquence en haute fréquence (Up converter). Réciproquement, les signaux haute fréquence sont translatés à basse fréquence pour être traités (Down converter).
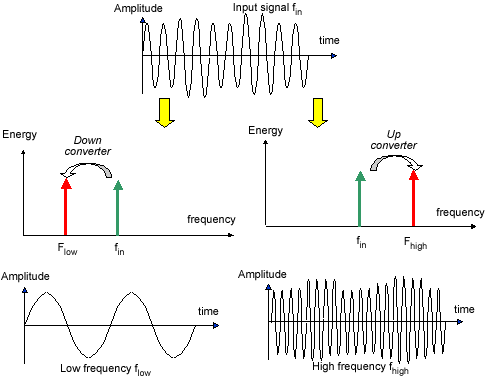
Ajout de deux sinusoïde
La somme de deux sinusoïdes se réalise simplement avec trois résistances:

La simulation suivante donne la somme de 2 signaux S1 et S2.

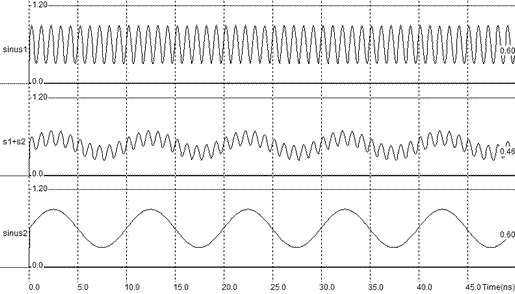
Sur la transformée de Fourier des signal S1+S2 on note 2 raies: une à la fréquence de S1 et l'autre à la fréquence de S2. L'addition de 2 sinusoïdes ne crée pas de fréquence supplémentaire.

Multiplication de 2 sinusoïdes
La multiplication de 2 sinusoïdes génère deux nouvelles fréquences: la première est constituée de la somme des 2 sinusoïdes, la deuxième de leur différence.
 |
| where ω1=2π.f1 ω2=2π.f2 f1 = frequency of signal 1 (Hz) f2 = frequency of signal 2 (Hz) |
Sur la figure suivante on a multiplié une sinusoïde de fréquence fin par une sinusoïde de fréquence fosc. On a généré 2 nouvelles raies: fosc-fin et fosc+fin. Pour éliminer la contribution de fosc-fin, par exemple, on peut utiliser un circuit résonnateur LC qui ne laissera passer que la raie fosc+fin.


Comment utiliser un MOS pour multiplier deux sinus
Les transistors MOS n'ont pas un comportement linéaire comme le montre la figure ci-dessous. Il existe une dépendance au carré de Ids avec Vgs-VT, pour des transistors de grande taille: W=50µm, L=0.5µm.
![]()

L'idée est la suivante:
On additionne 2 sinusoïdes fin et fosc sur la grille d'un MOS. Si VGS est la somme de 2 sinus on peut écrire:
 |
On retrouve dans l'expression de IDS deux nouvelles harmoniques fosc+fin et fosc-fin ce qui correspond à la multiplication des deux sinusoïdes. En résumé, additionner 2 sinusoïdes et les passer dans un circuit non linéaire crée une multiplication de ces sinusoïdes: on utilise ensuite un filtre pour éliminer les fréquences non désirées.


Implémentation
Le transistor N doit avoir un canal suffisamment long (L>0.5µm) pour avoir une dépendance carré entre VGS et IDS. On rajoute une résistance de charge de l'ordre du RON du MOS pour l'amplification. La simulation révèle une forme du signal de sortie très particulière.



Pour obtenir la transformé de Fourier il suffit de cliquer sur FFT dans Microwind.

Le signal désiré est situé à fin+fosc, soit 2450MHz. Seul un filtrage passe bande sélectif permettra de l'isoler des composants indésirables.
Mixeur avec résonnateur LC
Le mixeur de la figure suivante a deux particularités: on rajoute une inductance LHF de 3nH vers l'alimentation et une capacité CHF de 1-2pF en sortie. Ces 2 éléments forment un filtre passe bande à 2.45GHz.

Sur la transformée de Fourier de signal de sortie on perçoit clairement l'effet passe bande du résonnateur RC à 2.45GHz. Malheureusement ce filtre n'est pas assez sélectif pour éliminer les fréquences suivantes: fosc (2GHz), fos-fin (1.55GHz) et 2 fosc (4GHz).

En augmentant la fréquence d'entrée Fin on constate une augmentation de la fréquence de sortie de manière proportionnelle. En utilisant Microwind, on peut parametrer l'augmentation de fréquence comme le montre la figure suivante et visionner les résultats sur la FFT.


Mixeur
Le mixeur LC précédent n'étant pas assez sélectif (apparition de fosc-fin(1.55GHz), fosc (2GHz)), l'idée consiste à créer 2 signaux dont les harmoniques sont en opposition de phase avec les fréquences non désirés et en phase avec fosc-fin=1.55GHz et fosc+fin=2.45GHz. Le circuit est donné sur la figure suivante.
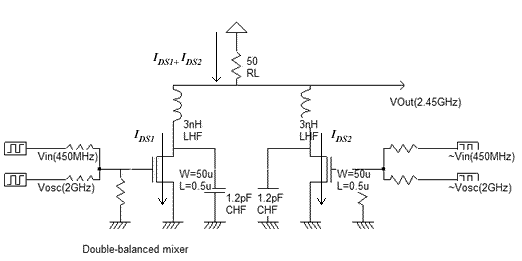
D'après les équations suivantes, on remarque que le courant qui traverse la resistance RL produit les harmoniques désirées fosc+fin et fosc-fin.
La FFT découlant de la simulation du circuit implémenté sur la figure suivante confirme la création des 2 harmoniques à 1.55 et 2.45GHz. L'avantage principal de ce circuit est l'élimination complète de l'oscillation à 2GHz. Seul le système d'addition à base de réseau de résistance est à revoir.


Mixeur de Gilbert
Ce type de mixeur, qui utilise 6 transistors comme le montre la figure suivante, permet de multiplier proprement deux sinusoïdes. Le réseau résistif a été éliminé, remplacé par des MOS inter-croisés.

Sur la simulation de la figure suivante, on peut voir qu'après 8ns la sortie Vout se stabilise. Sur la FFT de Vout (tracé en échelle logarithmique pour faire apparaître les harmoniques de faible amplitude), on remarque que les raies 2GHz (Fin) et 450MHz (Fosc) ont disparu et que le 2.45GHz apparaît clairement.


L'implémentation du mixeur de Gilbert est donné sur la figure suivante. On peut voir les deux spirales inductives de 3nH chacune, et de résistance intrinsèque de 6 Ohms. Ces spirales sont réalisées par un empilement de métal 4, metal 5 et métal 6.
Au centre on aperçoit les transistors MOS, et sur les côtés les capacités CHF.