Posez vos questions sur la première partie du cours ici
Bonjour, je comprend pas d'où vient le "dx" dans l'expression de l'intégrale, dans le cours il y a seulement Ao*exp(...).
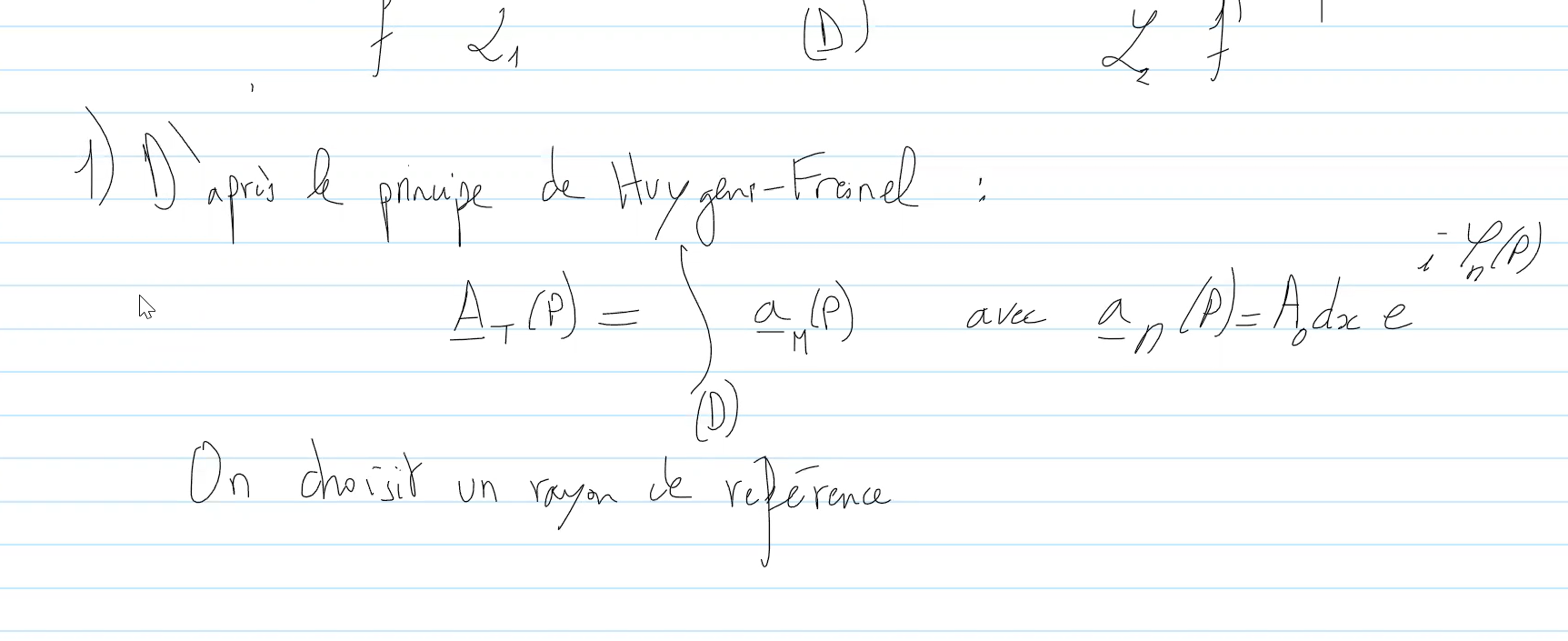
En fait, le "dx" est la traduction du principe de Huygens-Fresenl quand il est dit que l'amplitude de l'ondelette émise par les points sources secondaires est proportionnelle à un élément de surface dS autour du point. En coordonnée cartésienne, ce dS est égal à dx.dy . Dans cet exercice, l'invariance par translation selon (Oy) fait que "y" n'est pas une variable donc on ne considère pas la seconde dimension "y". Du coup, l'amplitude totale est l'intégrale de toutes les ondelettes dont l'amplitude de base est "un coefficient" x "dx". Il le coefficient est noté A0, ce qui n'est pas une très bonne idée car il fait référence à une amplitude. Or normalement, ce coefficient est une "amplitude par unité de longueur" pour obtenir un résultat homogène à la fin. Entre les résolution d'exercice et le cours, parfois le "dx" est implicitement intégré dans l'amplitude, parfois non mais avec un choix non pertinent dans les notations... Désolé pour la confusion. Savoir vérifier l'homogénéité permet de clarifier les expressions et le calcul.
Bonjour Monsieur,
Nous avons vu que pour satisfaire le critère de cohérence, nécessaire au phénomène d'Interférence, deux méthodes existaient.
Ces dernières sont :
-Méthode par division du front d'onde
-Méthode par division d'amplitude
Cependant, quelle(s) différence(s) y a-t-il entre ces deux méthodes, et en quoi consistent-elles ?
Je vous remercie.
La division d'amplitude consiste à utiliser un dispositif générant une onde réfléchie et une onde transmise qui vont ensuite se superposer (des fois on utilise des miroirs pour les renvoyer l'une sur l'autre). Ainsi les amplitudes de ces 2 ondes sont des fractions de l'amplitude de l'onde initiale (d'où le terme "division d'amplitude"). On cherche en général à avoir des coefficients de division d'amplitude qui sont égaux pour les 2 ondes (pour avoir un contraste max). On utilise par exemple des lames "semi-réfléchissantes" pour faire ça.
Bonjour,
Je vous écris car j'avais plusieurs question concernant les premiers chapitres du cours.
La première concerne la plaque en verre de l'exercice 2 de TD. Dans la séance de questions-réponses qui est sur Moodle, vous dites que nous considérons que les rayons sont para-axiaux car nous sommes dans le cadre de la théorie scalaire. Cependant, je n'arrive pas très bien à comprendre pourquoi un angle θ apparait lorsque le rayon sort de la plaque et ne redevient pas perpendiculaire à l'axe (Oz).
D'autre part, pour justifier de la cohérence temporelle, je comprends la raison pour laquelle le temps Td a été introduit, mais je ne saisis pas tout à fait de quelle façon nous nous en servons par la suite.
Enfin, concernant le phénomène de diffraction, il faut que l'ouverture par laquelle passe la fente soit petite pour qu'il se produise, mais je ne crois pas avoir compris comment quantifier cette taille là, ni de quelle façon justifier que le champ électrique total ne soit pas nul au point considéré de l'écran.
Vous serait-il possible de clarifier ces points-là ?
En vous remerciant,
Question 2 : le temps de la détection, c'est-à-dire le temps pendant lequel le détecteur intègre le signal reçu pour me donner la valeur de l'intensité, est grand devant la durée de vie des flashs, d'où la nécessité, si on veut observer une image stable, de superposer toujours les mêmes flashs... Bref, on explique l'intérêt des dispositifs interférentiels par division du front d'onde ou de l'amplitude à partir d'une unique source. On n'en parle plus après parce qu'on considère que le problème est réglé : en effet, puisque la mesure ne change plus, on peut intégrer le signal pendant le temps qu'on veut, on aura toujours la même valeur moyenne du vecteur de Poynting, et donc la même valeur d'intensité. finalement, peu importe la valeur de Td si on utilise des sources mutuellement cohérentes. Du coup, je n'ai plus, dans le cours, reparlé du temps d'intégration du détecteur....
Question 3 : La meilleure façon d'avoir une idée de l'importance du phénomène de diffraction est de regarder la taille de la tâche d'Airy. On sait que le terme qui est déterminant, que l'ouverture soit ronde ou rectangulaire, c'est le produit lambda*focale/ouverture. Si on prend une focale de 1 mètre, on voit tout de suite que si on fait passer la lumière issue d'un seul point source par une ouverture de taille caractéristique du même ordre de grandeur que lambda, alors lambda/lambda=1 et l'image du point est une tâche d'1 mètre de côté environ !!! En raison à l'inverse, la diffraction sera faible si l'ouverture est très grande devant lambda. Pour la justification de la diffraction, c'est directement le principe de Huygens-Fresnel et l'interférence du coup d'une infinité d'ondelette qui permet de l'expliquer par l'optique ondulatoire.
Je me permets de vous poser une nouvelle question sur les chapitres d'Interférence et de Diffraction.
J'ai cru comprendre que deux sources spatialement distinctes étaient incohérentes (critère de cohérence spatiale). Pour autant, le principe de Huygens-Fresnel précise que toutes les sources secondaires de l'ouverture sont mutuellement cohérentes et interfèrent entre elles. Comment se fait-il ?
Je vous remercie.
Pour la diffraction, justement, le principe de Huygens-Fresnel stipule que tous les points de l'ouverture sont des points sources secondaires cohérentes entre elles. Ce n'est donc pas du tout la même chose que pour une source lumineuse étendue (et le calcul est donc bien différent).
Je n'ai pas très bien compris le critère de Rayleigh, son énoncé et l'utilisation qu'on peut en faire. Pouvez-vous m'éclairer ? En vous remerciant par avance,
Manon JULIA