| Les circuits Radio-Fréquences > Inductances |
Les inductances sont généralement utilisées pour filtrer, amplifier ou créer des circuits résonnants pour des applications radio-fréquences.

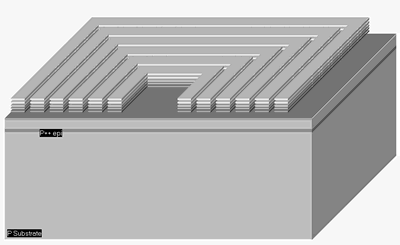
Une inductance intégrée se présente généralement sous la forme d'une spirale carrée. Parfois, certains procédés de fabrication n'acceptent que les angles à 90°. Cependant lorsque la technologie le permet on préfèrera réaliser une inductance avec des angles à 45° pour augmenter le facteur de qualité.
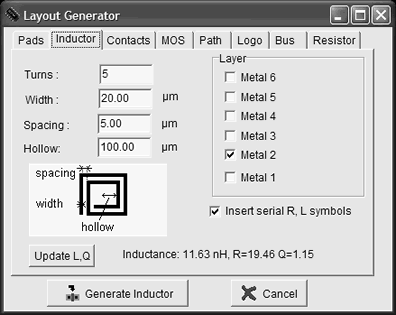
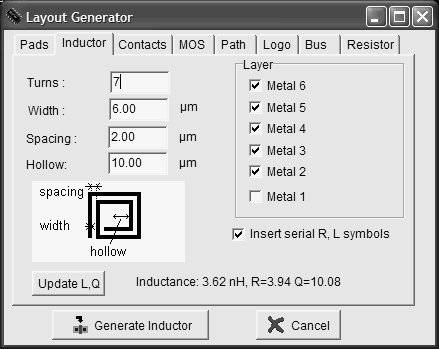
En utilisant le commande "Edit > Generate > Inductor" de Microwind nous avons réalisé une inductance de 12nH comme le montre la figure suivante. En bas à droite de la fenêtre "Layout Generator" apparaissent la valeur de l'inductance, de la résistance et du facteur de qualité Q.
Il existe dans la littérature plusieurs formulations de l'inductance. Microwind utilise une des equations les plus répandues ; celle donnée par M. Wheeler en 1928 et qui reste encore valable pour les inductances intégrées:
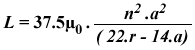 |
(Equ. 12-1) |
| with r = n.(w + s) µ0=4π.10-7 n=number of turns w= conductor width (m) s=conductor spacing (m) r=radius of the the coil (m) a=square spiral’s mean radius (m) | |
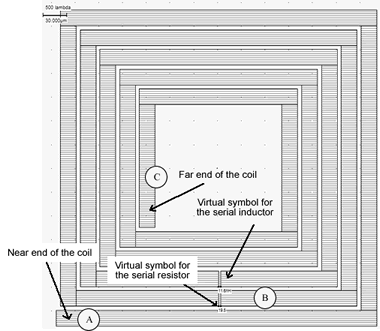
Le facteur de qualité permet de quantifier la résonance d'un circuit. Sa formulation n'est pas aussi facile qu'il en parait. Nous pouvons modéliser la spirale précédente comme une inductance L1 en série avec une résistance R1 et 2 capacites parasite vers la masse C1 et C2 comme sur la figure suivante.
Le facteur de qualité est donné dans ce cas par l'équation suivante:
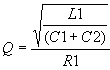 |
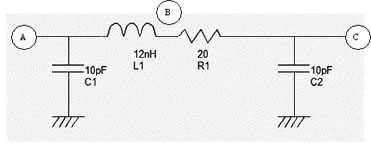 |
Pour l'inductance de 12nH, C1=C2=10pF et R1=20Ω, on trouve un facteur de qualité de 1.15.
Un facteur de qualité important est intéressant pour réaliser des gains en tension ainsi que des filtres fréquentiels avec une bonne sélectivité. Généralement Q est entre 3 et 30.
La résistance série R1 de la spirale ainsi que les capacités de couplages substrat C1 et C2 doivent être les plus petits possibles pour augmenter le facteur de qualité.
Pour cela on peut
 |
 |
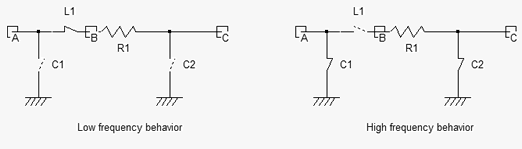
La spirale peut être considérée comme un circuit RLC résonant à basse fréquence, l'inductance se comporte comme un court-circuit et la capacité comme un circuit ouvert. Le potentiel du nœud C est alors égal à celui du nœud A si aucune charge n'est connectée au nœud C (aucun courant ne traverse R1).
A haute fréquence, l'inductance se comporte comme un circuit ouvert et la capacité comme un court-circuit. Il n'y a donc plus de connexion entre A et C.
A une certaine fréquence ƒr, le circuit se met à résonner. L'équation suivante permet de calculer la fréquence de resonance théorique du circuit.
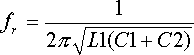
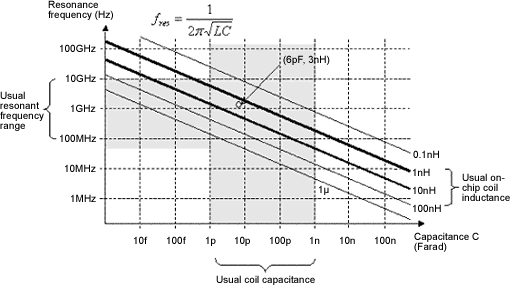
La figure suivante montre la variation de ƒr avec L et C. Pour les spirales intégrées la valeur de l'inductance varie généralement entre 1 et 100nH et la valeur de la capacité entre 1pF et 1nF. La frequence de résonance est alors comprise entre 100MHz et 10GHz.
Pour visualiser l'effet de la résonance et le facteur de qualité, il suffit d'appliquer une sinusoïde de faible amplitude (0.1V) sans offset sur le nœud A et d'augmenter petit à petit sa fréquence. La résonance s'observe quand le potentiel des nœuds B et C est supérieur à celui du nœud A. Le facteur de qualité est égal au ratio entre les tensions observées aux nœuds B et A.
Pour des fréquences inférieures à 100Hz, on utilise des spirales discrètes à cause de la grande valeur de l'inductance (1 à 100µH) impossible à intégrer sur silicium à cause de sa taille, donc de son coût.
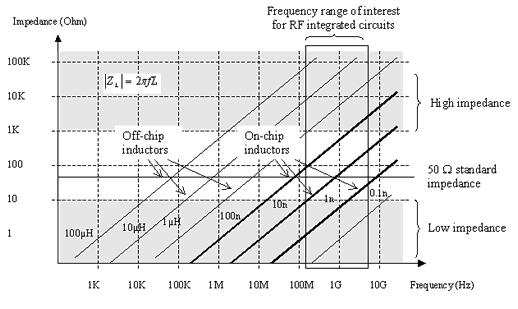
Les inductances intégrées ont une valeur comprise entre 1 et 100nH pour une fréquence de résonance comprise entre 300MHz et 3GHz. Par exemple, à 1GHz, une spirale dont l'inductance est de 10nH, s'adapte parfaitement aux entrées/sorties 50Ω des applications HF. Sur la figure suivante on peut lire l'impédance de la spirale en fonction de la fréquence.
| Les circuits Radio-Fréquences > Inductances |